5 Linear Response and Dynamical Correlation Functions
    5.1 Dynamics of the Statistical Operator: von Neumann's Equation
    5.2 Linear Response: Dynamical Susceptibility
    5.3 Spectral Representation
    5.4 Symmetries
    5.5 Mori's Scalar Product
    5.6 The Liouville Operator
Index

List of Figures

1 Dynamical processes in physical systems
2 Integration contour for the

Θ

-function

5 Linear Response and Dynamical Correlation Functions

Many dynamical processes induced by external perturbations of physical systems can be divided into three categories, namely (i) driving by external forces, (ii) relaxation from a partial to a global equilibrium, and (iii) probing by scattered 'particles'. See fig. 1

Figure 1: Dynamical processes in physical systems

All of these experimentally relevant situation can be described in terms of certain so-called correlation functions all of which are intimately related to each other.

For simplicity of notation we set

ℏ = k_{B} = 1

in the remainder of this chapter.

5.1 Dynamics of the Statistical Operator: von Neumann's Equation

Consider a quantum system

\tilde{H} = H + W (t)

(1)

and an arbitrary ensemble, described by a statistical operator

ρ_{S} (t) = \sum_{n} ρ_{n} | n, t ⟩ ⟨ n, t |,

(2)

where

| n, t ⟩

set the microstates in the Schrödinger picture with probabilities

ρ_{n}

. The time evolution of the microstates is governed by Schrödigner's equation

i \partial_{t} | n, t ⟩ = \tilde{H} | n, t ⟩ .

(3)

From this we get von Neumann's equation of motion for

ρ (t)

in the Schrödinger picture

\partial_{t} ρ_{S} (t) = - i \sum_{n} ρ_{n} [(\tilde{H} | n, t ⟩) ⟨ n, t | - | n, t ⟩ (⟨ n, t | \tilde{H})] = - i [\tilde{H}, ρ_{S} (t)] .

(4)

This can be translated into Heisenberg's picture

A_{H} (t) = e^{i \tilde{H} t} A (t) e^{- i \tilde{H} t}

| n, t ⟩_{S} = e^{i \tilde{H} t} | n, t ⟩ = | n, 0 ⟩_{S}

easily

ρ_{H} (t) = ρ_{S} (0),

(5)

and finally in the Dirac or interaction picture

A_{D} (t) = e^{iHt} A (t) e^{- iHt}

| n, t ⟩_{D} = e^{iHt} | n, t ⟩

\begin{matrix} \partial_{t} ρ_{D} (t) & = & iH ρ_{D} (t) - i ρ_{D} (t) H - i [H + W_{D} (t), ρ_{D} (t)] \\ = & - i [W_{D} (t), ρ_{D} (t)], & (6) \end{matrix}

where

W_{D} (t) = e^{iHt} W (t) e^{- iHt}

is the interaction in Dirac's picture.

Eqn. (6) seem particularly suited for perturbative approximations since the r.h.s. is proportional to

W

. We consider a case, in which

W (t)

is adiabatically switched in starting from

t = - \infty

W (t \to - \infty) = 0 ö ff " .

(7)

Therefore at

t = - \infty

the system is in equilibrium and

[ρ_{S} (- \infty), H] = 0,

(8)

with a canonical distribution function

ρ \equiv ρ_{S} (- \infty) = \frac{1}{Z} e^{- β H} = ρ_{D} (- \infty),

(9)

where the last equality follows from eqn. (8) and

A_{D} (t) = e^{iHt} A (t) e^{- iHt}

. From eqn. (6) we therefore get

\begin{matrix} ρ_{D} (t) & = & ρ - i \int_{- \infty}^{t} [W_{D} (t'), ρ_{D} (t)] dt = \\ = & ρ - i \int_{- \infty}^{t} [W_{D} (t'), ρ] dt + O (W^{2}) & (10) \end{matrix}

5.2 Linear Response: Dynamical Susceptibility

Let us consider a situation in which the perturbation

W (t)

is due to generalized external forces

$W (t) = - \sum_{ν} A_{ν} f_{ν} (t),$ $(11)$
where the

f_{ν} (t)

correspond to the forces and the operators

A_{ν}

refer to the generalized coordinates. Many such pairs of

(A_{ν}, f_{ν} (t))

are relevant in practical applications: (real space, momentum), (magnetization, magnetic field), (electric dipole, electric field), (electric current density, vector potential), (charge density, electric field), and so on. We now consider the response of the expectation value of

⟨ A_{μ}^{+} (t) ⟩

to linear order in the

W

\begin{matrix} δ ⟨ A_{μ}^{+} (t) ⟩ & = & ⟨ A_{μ}^{+} (t) ⟩ - ⟨ A_{μ}^{+} (- \infty) ⟩ \\ = & Tr {A_{μ D}^{+} (t) (ρ_{D} (t) - ρ_{D} (- \infty))} \\ = & - i \int_{- \infty}^{t} Tr {A_{μ D}^{+} (t) [W_{D} (t'), ρ]} dt + O (W^{2}) \\ = & i \sum_{ν} \int_{- \infty}^{t} Tr {ρ [A_{μ D}^{+} (t), A_{ν D} (t')]} f_{ν} (t') dt' \\ = & i \sum_{ν} \int_{- \infty}^{t} ⟨ [A_{μ D}^{+} (t), A_{ν D} (t')] ⟩_{ρ} f_{ν} (t') dt', & (12) \end{matrix}

where we have dropped terms of

O (W^{2})

In the remainder of section 5 time dependencies will usually refer to the Dirac picture, or speaking differently the Heisenberg picture for

W = 0

. Moreover statistical averages will be formed w.r.t. to the equilibrium statistical operator

ρ

t = - \infty

from eqn. (9). We will therefore drop the subscripts '

D

' and '

ρ

' in expressions like eqn. (12).

Using eqn. (12) we define the dynamical susceptibility

$χ_{μ ν} (t, t') = i Θ (t - t') ⟨ [A_{μ}^{+} (t), A_{ν} (t')] ⟩ \equiv 2 i Θ (t - t') χ_{μ ν}^{''} (t, t') .,$ $(13)$
where we have introduced to so-called spectral function $χ_{μ ν}^{''} (t, t')$ . Because of the

Θ

-function we may write

δ ⟨ A_{μ}^{+} (t) ⟩ = \sum_{ν} \int_{- \infty}^{\infty} χ_{μ ν} (t, t') f_{ν} (t') dt' .

(14)

Obviously this extends the meaning of a susceptibility from static thermodynamics to dynamical phenomena. If we assume that the coordinates

A_{μ}

are time-independent in the Schrödinger picture, then we have

\begin{matrix} ⟨ [A_{μ}^{+} (t), A_{ν} (t')] ⟩ & = & Tr {ρ [e^{iHt} A_{μ}^{+} e^{- iHt}, e^{iHt'} A_{ν} e^{- iHt}]} \\ = & Tr {ρ [e^{iH (t - t')} A_{μ}^{+} e^{- iH (t - t')}, A_{ν}]} \\ = & ⟨ [A_{μ}^{+} (t - t'), A_{ν}] ⟩, & (15) \end{matrix}

i.e. the dynamical susceptibility is a function of the time-difference only

χ_{μ ν}^{('')} (t, t') = χ_{μ ν}^{('')} (t - t', 0) \equiv χ_{μ ν}^{('')} (t - t') .

(16)

Example 1 Let us consider a harmonic oscillator under the influence of an external driving force which acts on its displacement coordinate

$\begin{matrix} \tilde{H} & = & ω_{0} b^{+} b + (b^{+} + b) f (t) & (17) \\ = & \overset{⏞}{H} + \overset{⏞}{W (t)} . \end{matrix}$

For bosons we ave $[b, b^{+}] = 1$ . Note that

$b^{+} + b \propto \hat{r},$ $(18)$
where $\hat{r} = {\hat{r}}^{+}$ is the displacement coordinate of the oscillator. The time dependence in the Dirac picture is obtained from $b_{D} (t) = e^{iHt} {be}^{- iHt}$ , or

$\begin{matrix} \partial_{t} b_{D} (t) & = & {ie}^{iHt} [H, b] e^{- iHt} = i ω_{0} e^{iHt} [b^{+} b, b] e^{- iHt} \\ = & i ω_{0} e^{iHt} (b^{+} [b, b] + [b^{+}, b] b) e^{- iHt} \\ = & - i ω_{0} e^{iHt} {be}^{- iHt} = - i ω_{0} b_{D} (t) . & (19) \end{matrix}$

This DEQN can be solved by direct integration and taking into account that $b_{D} (0) = b$

$\begin{matrix} b_{D} (t) & = & e^{- i ω_{0} t} b & (20) \\ b_{D}^{+} (t) & = & e^{i ω_{0} t} b^{+} & (21) \end{matrix}$

where the hermitean conjugate has yield a corresponding equation for the creation operator. Inserting this into eqn. (15) we get an expression for the displacement susceptibility

$\begin{matrix} χ_{rr} (t) & = & i Θ (t) ⟨ [e^{i ω_{0} t} b^{+} + e^{- i ω_{0} t} b, b^{+} + b] ⟩ \\ = & i Θ (t) (e^{i ω_{0} t} ⟨ [b^{+}, b] ⟩ + e^{- i ω_{0} t} ⟨ [b, b^{+}] ⟩) \\ = & i Θ (t) (e^{- i ω_{0} t} - e^{i ω_{0} t}) . & (22) \end{matrix}$

Note in passing that it is due to the particular simplicity of this example, that the dynamical susceptibility is completely temperature independent.

5.3 Spectral Representation

The description of dynamical phenomena involves many different types of functions, mathematically similar to eqn. (13). As we continue we will find, that these function are all determined by the spectral function. Let us consider the Laplace transform of $χ_{μ ν} (t)$ , dropping the subscripts for simplicity

\begin{matrix} χ (z) & = & \int_{0}^{\infty} dt e^{izt} χ (t) = \int_{- \infty}^{\infty} dt 2 {ie}^{izt} Θ (t) χ^{''} (t), & (23) \end{matrix}

where

Im (z) > 0

. Note that the following applies to any pair of functions $χ (t)$ and $χ^{''} (t)$ related trough eqn. (13). Now, from the residue theorem (see fig. 2)

Figure 2: Integration contour for the

Θ

-function

\int_{- \infty}^{\infty} \frac{d ω}{π} \frac{e^{i ω t}}{ω - z} = {\begin{matrix} 2 {ie}^{izt} & t > 0 \\ 0 & t < 0 \end{matrix},

(24)

i.e. we may write

χ (z) = \int_{- \infty}^{\infty} dt χ^{''} (t) \int_{- \infty}^{\infty} \frac{d ω}{π} \frac{e^{i ω t}}{ω - z} = \int_{- \infty}^{\infty} \frac{d ω}{π} \frac{χ^{''} (ω)}{ω - z},

(25)

where

χ^{''} (ω)

is the Fourier transform of

χ^{''} (t)

. The preceding equation is called a spectral representation of

χ (z)

. It is used to define the retarted / advanced dynamical susceptibilities

χ^{R / A} (u) = χ (u \pm i 0^{+}) = [P \int_{- \infty}^{\infty} \frac{d ω}{π} \frac{χ^{''} (ω)}{ω - u}] \pm i χ^{''} (u) \equiv χ^{'} (u) \pm i χ^{''} (u),

(26)

where we have used

1 / (x \pm i 0^{+}) = P 1 / x \pm i δ (x)

, moreover we have defined the real part

χ^{'} (u)

. Eqn. (26) is called the Kramer-Kronig transformation(representation) of the retarded / advanced susceptibility. Note that while in the derivation of eqn. (25) we needed that

Im (z) > 0

, we may nevertheless 'use' eqn. (25) also as a definition in for the case of

Im (z) < 0

. That is how we mathematically extend its usage in the definition of

χ^{A} (u)

With eqn. (16), eqn. (14) is of convolution form and suggest a simple Fourier transform. However some care has to be exercised because of the

Θ

-function which renders the direct Fourier transform of

χ (t)

delicate. Consider first

\begin{matrix} \int_{- \infty}^{\infty} dt e^{i ω t} 2 i Θ (t) χ^{''} (t) = \int_{- \infty}^{\infty} e^{i ω t} \int_{- \infty}^{\infty} \frac{d ω'}{π} \frac{e^{i ω' t}}{ω' - i 0^{+}} χ^{''} (t) dt & (27) \\ = & \int_{- \infty}^{\infty} \frac{d ω'}{π} \frac{1}{ω' - i 0^{+}} \int_{- \infty}^{\infty} e^{i (ω + ω') t} χ^{''} (t) dt = \int_{- \infty}^{\infty} \frac{d ω'}{π} \frac{χ^{''} (ω')}{ω' - (ω + i 0^{+})} = χ^{R} (ω) . \end{matrix}

I.e., the because the

Θ

-function is a distribution (like the

δ

-function), the Fourier transform of

χ (t)

is not simply

χ (ω)

but

χ^{R} (ω)

. Using this, eqn. (14,16), and the convolution-theorem, and re-introducing the subscripts we get

δ ⟨ A_{μ}^{+} (ω) ⟩ = \sum_{ν} χ_{μ ν}^{R} (ω) f_{ν} (ω) .

(28)

Apart from the case of a driving force at frequency

ω

, as in eqn. (28), another important case is that of a perturbation switched on adiabatically i.e. infinitesimally slow up to

t = 0

f_{ν} (t) = Θ (- t) e^{0^{+} t} f_{ν} .

(29)

In that case, one is interested in the response at

t = 0

\begin{matrix} δ ⟨ A_{μ}^{+} (t = 0) ⟩ & = & \sum_{ν} \int_{- \infty}^{0} χ_{μ ν} (0 - t') e^{0^{+} t'} f_{ν} dt' = \sum_{ν} \int_{0}^{\infty} χ_{μ ν} (t') e^{- 0^{+} t'} dt' f_{ν} \\ = & \sum_{ν} χ_{μ ν}^{R} (ω = 0) f_{ν} \equiv \sum_{ν} χ_{μ ν}^{Iso} f_{ν} & (30) \end{matrix}

χ_{μ ν}^{Iso}

is called the isolated/adiabatic susceptibility. It is very tempting to associate this susceptibility with the isothermal susceptibility

χ_{μ ν}^{T} = \frac{\partial ⟨ A_{μ}^{+} ⟩}{\partial f_{ν}} .

(31)

from static thermodynamics. However this is wrong, as

χ_{μ ν}^{Iso} \neq χ_{μ ν}^{T}

in general, as we will see later.

Example 2 Let us apply the preceding to the results from example 1. From eqn. (22) we get

$χ_{rr}^{''} (t) = \frac{1}{2} (e^{- i ω_{0} t} - e^{i ω_{0} t}),$ $(32)$
and from that

$\begin{matrix} χ_{rr}^{''} (ω) & = & \frac{1}{2} \int_{- \infty}^{\infty} e^{i ω t} (e^{- i ω_{0} t} - e^{i ω_{0} t}) dt \\ = & π [δ (ω - ω_{0}) - δ (ω + ω_{0})], & (33) \end{matrix}$

i.e., the Fourier transform of the spectral function has 'peaks' at the excitation energy of the system. Therefore it is frequently called 'the spectrum' of the system. The retarded / advanced susceptibility follows from the spectral representation eqn. (25)

$\begin{matrix} χ_{rr}^{R / A} (ω) & = & \int_{- \infty}^{\infty} \frac{δ (ω - ω_{0}) - δ (ω + ω_{0})}{ω' - ω \mp i 0^{+}} d ω' = \\ = & \frac{2 ω_{0}}{ω_{0}^{2} - (ω \mp i 0^{+})^{2}}, & (34) \end{matrix}$

from which we can deduce the isolated susceptibility

$χ_{rr}^{Iso} = \frac{2}{ω_{0}} .$ $(35)$
For $ω_{0} \to 0$ the system gets 'soft', i.e. it is physically clear, that in this situation its response to an adiabatic perturbation will diverge - as in eqn. (35).
Exercise 3 Assume $χ^{''} (ω) = 2 \sqrt{1 - ω^{2}} \cdot Θ (1 - ω^{2})$ . Calculate $χ (z)$ from eqn. (25). Verify, that eqn. (26) is satisfied, regarding $χ^{''} (ω)$ . Plot $χ^{' ('')} (ω)$ . Discuss the large- $ω$ behavior of $χ^{R} (ω)$ .

5.4 Symmetries

The symmetries of

χ_{μ ν}^{('')} (ω)

are of great importance. For eg., they serve as consistency checks, both for experiments and theories, they restrict the allowed forms that susceptibilities can take on, and they lead to reciprocity relations between various types of responses, just to name a few. To simplify the notation we define

A_{μ}^{+} = A_{\overline{μ}}

(36)

Complex conjugation

χ_{μ ν}^{''} (ω)^{☆} = - χ_{\overline{μ} \overline{ν}}^{''} (- ω) .

(37)

Proof

\begin{matrix} χ_{μ ν}^{''} (ω)^{☆} & = & {[\int_{- \infty}^{\infty} e^{i ω t} \frac{1}{2} ⟨ [A_{μ}^{+} (t), A_{ν}] ⟩ dt]}^{☆} = \int_{- \infty}^{\infty} e^{- i ω t} \frac{1}{2} ⟨ [A_{μ}^{+} (t), A_{ν}] ⟩^{☆} dt & (38) \\ = & \int_{- \infty}^{\infty} e^{- i ω t} \frac{1}{2} ⟨ [A_{ν}^{+}, A_{μ}^{+ +} (t)] ⟩ dt = - \int_{- \infty}^{\infty} e^{- i ω t} \frac{1}{2} ⟨ [A_{μ}^{+ +} (t), A_{ν}^{+}] ⟩ dt = - χ_{\overline{μ} \overline{ν}}^{''} (- ω) \end{matrix}

where we have used

⟨ A ⟩^{☆} = ⟨ A^{+} ⟩

and

(A_{μ}^{+} (t {))}^{+} = A_{μ}^{+ +} (t)

Commutator

χ_{μ ν}^{''} (ω) = - χ_{\overline{ν} \overline{μ}}^{''} (- ω) .

(39)

Proof

\begin{matrix} χ_{μ ν}^{''} (ω) & = & \int_{- \infty}^{\infty} e^{i ω t} \frac{1}{2} ⟨ [A_{μ}^{+} (t), A_{ν}] ⟩ dt = - \int_{- \infty}^{\infty} e^{i ω t} \frac{1}{2} ⟨ [A_{ν}, A_{μ}^{+} (t)] ⟩ dt & (40) \\ = & - \int_{- \infty}^{\infty} e^{i ω t} \frac{1}{2} ⟨ [A_{ν}^{+ +} (- t), A_{μ}^{+}] ⟩ dt = - \int_{- \infty}^{\infty} e^{- i ω t} \frac{1}{2} ⟨ [A_{ν}^{+ +} (t), A_{μ}^{+}] ⟩ dt = - χ_{\overline{ν} \overline{μ}}^{''} (- ω) . \end{matrix}

For

A_{μ} = A_{ν} \equiv A

and

A^{+} = A

we get

χ^{''} (ω) = - χ^{''} (- ω)

, i.e. in that case the spectral function is real and odd in frequency.

Time inversion is a linear operation which needs some introduction, which for completeness will be included here. In its coordinate representation any solution

ψ (r, t)

of the one-particle Schrödinger equation has the following symmetry

i \partial_{t} ψ (r, t) = [\frac{p^{2}}{2 m} + V (r)] ψ (r, t) \Leftrightarrow i \partial_{t} ψ^{☆} (r, - t) = [\frac{p^{2}}{2 m} + V (r)] ψ^{☆} (r, - t),

(41)

which can easily be generalized to many particles. I.e. for states "inversion of time + complex conjugation" is a symmetry of the Schrödinger equation. Under time inversion the operators 'space'

r

and 'momentum'

p

change according to

Π r Π^{- 1} = r Π p Π^{- 1} = - p .

(42)

For

[r, p]

to be invariant under

Π

, the following has to hold

\begin{matrix} - i & = & [r, - p] = [Π r Π^{- 1}, Π p Π^{- 1}] = Π [r, p] Π^{- 1} = Π i Π^{- 1} \\ \Rightarrow - i Π & = & Π i, & (43) \end{matrix}

which is generalized into the requirement

a^{☆} Π = Π a,

(44)

i.e. time inversion is anti-linear.

While the adjoint of any linear operator is given by

⟨ μ | A ν ⟩ = ⟨ ν | A^{+} μ ⟩^{☆} = ⟨ A^{+} μ | ν ⟩,

(45)

(where we have used von-Neumann's notation for scalar products instead of Dirac's) it will turn out to be reasonable to define the so-called anti-adjoint

⟨ Π^{+} μ | ν ⟩^{☆} \equiv ⟨ μ | Π ν ⟩ .

(46)

From this and the requirement that the norm is conserved under

Π

- which is consistent eqn. (45) we get

\begin{matrix} ⟨ Π μ | Π μ ⟩ & = & ⟨ Π^{+} Π μ | μ ⟩^{☆} \equiv ⟨ μ | μ ⟩^{☆} = ⟨ μ | μ ⟩ & (47) \\ \Rightarrow Π^{+} Π = 1 & Π^{- 1} Π = Π Π^{- 1} = Π^{+} Π = Π Π^{+} = 1 . & (48) \end{matrix}

It is important to realize that in view of eqn. (41) it is the 2nd equal sign in eqn. (47) which is consistent with eqn. (46) but not with eqn. (45). This is the reason for introducing the anti-adjoint. In turn time inversion is anti-unitary.

Now we assume, that

H

and

ρ

are invariant under

Π

[H, Π^{(- 1, +)}] = [ρ, Π^{(- 1, +)}] = 0 .

(49)

Applying this on the spectral function in the time-domain and dropping the subscripts

μ, ν

for this

\begin{matrix} Tr {ρ [A (t), B (t')]} = \sum_{n} ⟨ n | Π^{+} Π ρ [A (t), B (t')] n ⟩ = \sum_{n} ⟨ Π n | Π ρ [A (t), B (t')] n ⟩^{☆} \\ = & \sum_{n} ⟨ Π n | Π ρ [A (t), B (t')] Π^{+} Π n ⟩^{☆} = \sum_{n} ⟨ Π n | ρ [Π A (t) Π^{+}, Π B (t') Π^{+}] Π n ⟩^{☆} . & (50) \end{matrix}

Since

| n ⟩

in the preceding is a complete orthonormal set (COS),

| Π n ⟩

is also and we may replace it by

| n ⟩

in the trace. Many operators have a so-called parity

ε

w.r.t. certain operations like time-reversal

Π

or (real-space) inversion

P

, i.e.

\begin{matrix} Π A (t) Π^{- 1} & = & ε^{t} A (- t) & (51) \\ PA (t) P^{- 1} & = & ε^{P} A (t) . & (52) \end{matrix}

Typical examples are coordinate

r

with

ε^{P} = - 1

and

ε^{t} = 1

, or velocity

v

with

ε^{P} = - 1

and

ε^{t} = - 1

, or (electric/)magnetic field (

E

B

with

ε^{P} = (- 1 /) - 1

and

ε^{t} = (1 /) - 1

. In the following we restrict ourselves to such. Then eqn. (50) continues as

= ε_{A}^{t} ε_{B}^{t} \sum_{n} ⟨ n | ρ [A (- t), B (- t')] n ⟩^{☆} = ε_{A}^{t} ε_{B}^{t} χ_{AB} (- t, - t')^{☆} = - ε_{A}^{t} ε_{B}^{t} χ_{\overline{A} \overline{B}} (- t, - t') .

(53)

In the frequency domain assuming eqn. (16) and returning to the subscripts we get

χ_{μ ν} (ω) = - ε_{μ}^{t} ε_{ν}^{t} χ_{\overline{μ} \overline{ν}} (- ω) .

(54)

Example 4 Consider the spectral function from examples 1 and 2

$χ_{rr}^{''} (ω) = π [δ (ω - ω_{0}) - δ (ω + ω_{0})] .$ $(55)$
Within the notation of eqn. (36) we have $\overline{r} = r^{+} = r$ . From this
The commutator rule

$χ_{rr}^{''} (ω) = - χ_{\overline{r} \overline{r}}^{''} (- ω) = - χ_{rr}^{''} (- ω)$ $(56)$
is obviously satisfied. The complex conjugation rule

$χ_{rr}^{''} (ω)^{☆} = χ_{rr}^{''} (ω)^{☆} = - χ_{rr}^{''} (- ω)$ $(57)$
sets $χ_{rr}^{''} (ω)$ to be real and odd in $ω$ . Finally, the t-reversal rule together with $ε_{r}^{t} = + 1$

$χ_{rr}^{''} (ω) = - (+ 1) (+ 1) χ_{rr}^{''} (- ω)$ $(58)$
leads to no additional insight.
Symmetries allow practically relevant conclusions about the vanishing of certain susceptibilities. Consider eg. the isolated (momentum $p$ ,real-space $r$ )-susceptibility

$χ_{pr}^{Iso} .$ $(59)$
From t-reversal we get

$χ_{pr}^{''} (ω) = - (- 1) (+ 1) χ_{pr}^{''} (- ω) = χ_{pr}^{''} (- ω) .$ $(60)$
Contrast this against eqn. (58) ! I.e. $χ_{pr}^{''} (ω)$ is even in $ω$ . Using eqn. (27,30) we get

$χ_{pr}^{Iso} = \int_{- \infty}^{\infty} \frac{d ω'}{π} \frac{χ_{pr}^{''} (ω')}{ω'} = 0 .$ $(61)$
A similar argument leads to $χ_{ME}^{Iso} = 0$ and $χ_{PB}^{Iso} = 0$ , for a time-inversion symmetric $H$ and $ρ$ , where $E (B)$ and $P (M)$ are the electric(magnetic) field and the electric polarization (magnetization).
At first sight, generating a magnetic moment with an electric field seems counter-intuitive anyway. However, to allow for $χ_{ME}^{Iso} \neq 0$ or $χ_{PB}^{Iso} \neq 0$ a system simply has to break time-inversion symmetry. By the famous P(arity) C(harge conjugation) T(ime inversion)-theorem, this is synonymous to the breaking of parity (i.e. space inversion symmetry) in most cases. Solids which display such symmetry loss are also called non-centro-symmetric.
Exercise 5 (Real space) Inversion Consider the $r$ -dependent operators

i) density	$\hat{n} (r) = \sum_{l} δ (r - {\hat{R}}_{l})$
ii) momentum density	$\hat{p} (r) = \sum_{l} δ (r - {\hat{R}}_{l}) {\hat{p}}_{l}$
iii) spin density	$\hat{S} (r) = \sum_{l} δ (r - {\hat{R}}_{l}) {\hat{S}}_{l}$

of an

N

-particle system, with

l = 1 \dots N

, where the '

\hat{}

' refers to operators and

r

is a real space coordinate.

a) Use that under inversion $P {\hat{R}}_{l} P^{- 1} = - {\hat{R}}_{l}$ , $P {\hat{p}}_{l} P^{- 1} = - {\hat{p}}_{l}$ , and

P {\hat{S}}_{l} P^{- 1} = {\hat{S}}_{l}

to show that

PA (r) P^{- 1} = ε_{A}^{P} A (- r),

(62)

for

A (r) = \hat{n} (r)

\hat{p} (r)

and

\hat{S} (r)

, with

ε_{n}^{P} = 1

ε_{p}^{P} = - 1

, and

ε_{S}^{P} = 1

b) Assume a statistical operator

ρ

invariant under inversion

[ρ, H] = 0

. Defining the the real-space dependent spectral function

χ_{μ ν} (r, t; r', t') \equiv i Θ (t - t') ⟨ [A_{μ}^{+} (r, t), A_{ν} (r', t')] ⟩

, show that in this case

χ_{μ ν} (r, t; r', t') = ε_{μ}^{P} ε_{ν}^{P} χ_{μ ν} (- r, t; - r', t') .

(63)

As a consequence, assuming translational invariance and a time independent Hamilton operator, i.e.

χ_{μ ν} (r, t; r', t') = χ_{μ ν} (r - r', t - t')

, show that the Fourier transform into wave vector (i.e.

q

) and frequency (i.e.

ω

) space satisfies

χ_{μ ν} (q, ω) = ε_{μ}^{P} ε_{ν}^{P} χ_{μ ν} (- q, ω) .

(64)

c) Use eqn. (30) to and eqn. (64) to derive the isolated susceptibilities

χ_{np}^{Iso} (r = 0)

and

χ_{sp}^{Iso} (r = 0)

. What is the physical significance of this.

5.5 Mori's Scalar Product

We may define the following mapping from the vector space of linear operators

A_{μ}

on the scalar space of complex numbers into the complex numbers

\begin{matrix} ⟨ A_{μ} | A_{ν} ⟩ & = & \int_{0}^{β} ⟨ Δ A_{μ}^{+} (τ) Δ A_{ν} ⟩ d τ & (65) \\ β & = & 1 / T \\ Δ A & = & A - ⟨ A ⟩ & (66) \\ A (τ) & = & e^{τ H} {Ae}^{- τ H} τ \in Re . & (67) \end{matrix}

Here

τ

is called 'imaginary' time. Note, that unlike for real time

[A (τ {)]}^{+} \neq A^{+} (τ)

. The brackets on the r.h.s

⟨ ⟩

are usual thermal averages. The brackets

⟨ \dots | \dots ⟩

on the l.h.s. of eqn. (65) should not be confused with a scalar product of quantum mechanical states. Yet, this so-called Mori product satisfies all properties of a conventional scalar product, i.e. it is:
i) Bilinear: this is trivial
ii) Positive semi-definite: (w.l.o.g. set

⟨ A ⟩ = 0

)

\begin{matrix} ⟨ A | A ⟩ & = & \int_{0}^{β} ⟨ A^{+} (τ) A ⟩ d τ = \frac{1}{Z} \sum_{lm} \int_{0}^{β} e^{- β E_{l}} ⟨ l | A^{+} (τ) | m ⟩ ⟨ m | A | l ⟩ d τ \\ = & \frac{1}{Z} \sum_{lm} e^{- β E_{l}} ⟨ l | A^{+} | m ⟩ ⟨ m | A | l ⟩ \int_{0}^{β} e^{τ (E_{l} - E_{m})} d τ \\ = & \frac{1}{Z} \sum_{E_{m} \neq E_{n}} | ⟨ m | A | l ⟩ |^{2} \frac{e^{- β E_{m}} - e^{- β E_{l}}}{E_{l} - E_{m}} + \frac{β}{Z} \sum_{E_{m} = E_{n}} | ⟨ m | A | l ⟩ |^{2} . & (68) \end{matrix}

Both sums on the last line contain only positive addends. Moreover if, and only if all matrix elements of

A

are zero, i.e.

A = 0

, then

⟨ A | A ⟩ = 0

. q.e.d.
iii) Complex conjugation:

\begin{matrix} ⟨ A | B ⟩^{☆} & = & \int_{0}^{β} ⟨ A^{+} (τ) B ⟩^{☆} d τ = \int_{0}^{β} Tr {ρ A^{+} (τ) B}^{☆} d τ = \int_{0}^{β} Tr {B^{+} [A^{+} (τ {)]}^{+} ρ} d τ \\ = & \int_{0}^{β} Tr {B^{+} A (- τ) ρ} d τ = \int_{0}^{β} Tr {B^{+} (τ) A ρ} d τ = ⟨ B | A ⟩ . & (69) \end{matrix}

Mori's product has many applications in statistical mechanics. The first one applies to the isothermal susceptibility

χ_{μ ν}^{T} = \frac{\partial ⟨ A_{μ}^{+} ⟩}{\partial f_{ν}} = ⟨ A_{μ} | A_{ν} ⟩ .

(70)

The high-temperature limit

β \to 0

and also the classical case, i.e.

[H, A_{μ}] = 0

, of this equation can be read of easily from eqn. (65)

χ_{μ ν}^{T} \binom{\to}{\binom{β \to 0 or}{[H, A_{μ}] = 0}} \frac{⟨ Δ A_{μ}^{+} Δ A_{ν} ⟩}{T} .

(71)

This is the famous relation proportionality between fluctuations and susceptibilities. Eg. for a magnetic system in this limit we have

χ^{T} = ⟨ (Δ S)^{2} ⟩ / T

, which is simply Curie's law. The general proof of eqn. (70) is left to exercise 8.

Exercise 6 Given two operators with $A_{μ}^{+} = A_{μ}$ and $A_{ν}^{+} = A_{ν}$ . Show that $⟨ A_{μ} | A_{ν} ⟩ = ⟨ A_{ν} | A_{μ} ⟩$ . I.e. for hermitean operators, and because of eqn. (69), Mori's product is real.
Example 7 Let's continue with the harmonic oscillator. Analogous to eqn. (19) we get from eqn. (67)

$\begin{matrix} b (τ) & = & e^{- ω_{0} τ} b \\ b^{+} (τ) & = & e^{ω_{0} τ} b^{+} . & (72) \end{matrix}$

Using that $⟨ b ⟩ = ⟨ b^{+} ⟩ = 0$ , and inserting into eqn. (65) we get

$\begin{matrix} ⟨ r | r ⟩ & = & \int_{0}^{β} ⟨ (e^{ω_{0} τ} b^{+} + e^{- ω_{0} τ} b) (b^{+} + b) ⟩ d τ \\ = & \int_{0}^{β} e^{ω_{0} τ} ⟨ b^{+} b ⟩ d τ + \int_{0}^{β} e^{- ω_{0} τ} ⟨ {bb}^{+} ⟩ d τ \\ = & n (β) (\frac{1}{ω_{0}}) (e^{ω_{0} β} - 1) + (1 + n (β)) (- \frac{1}{ω_{0}}) (e^{- ω_{0} β} - 1) \\ = & \frac{1}{ω_{0}} + \frac{1}{ω_{0}} = \frac{2}{ω_{0}} & (73) \end{matrix}$

where we have used $⟨ bb ⟩ = ⟨ b^{+} b^{+} ⟩ = 0$ , and $⟨ b^{+} b ⟩ = n (β) = 1 / (e^{β ω_{0}} - 1)$ , and $[b, b^{+}] = 1$ .
From this and eqns. (35,71) we can read off that

$χ_{rr}^{Iso} = χ_{rr}^{T}$ $(74)$

Exercise 8 Thermodynamic perturbation theory. Prove eqn. (70)
a) TODO
b)
c)

5.6 The Liouville Operator

The time-evolution resulting from the equations of motion for operators in the Heisenberg picture can be brought into a form formally similar to that of states in the Schrödinger picture by introducing a so-called super operator, the Liouville operator

L

, which by definition is an operator acting on operators

\begin{matrix} {LA}_{μ} (t) & \equiv & [H, A_{μ} (t)] & (75) \\ \Rightarrow \frac{d}{dt} A_{μ} (t) & = & {iLA}_{μ} (t) & (76) \\ A_{μ} (t) & = & e^{iLt} A_{μ} . & (77) \end{matrix}

The Liouville operator is hermitean w.r.t. to the Mori product (w.l.o.g.

⟨ A ⟩ = ⟨ B ⟩ = 0

)

\begin{matrix} ⟨ A | LB ⟩ & = & \int_{0}^{β} ⟨ A^{+} (τ) LB ⟩ d τ = \int_{0}^{β} ⟨ e^{τ H} A^{+} e^{- τ H} [H, B] ⟩ d τ = \int_{0}^{β} ⟨ e^{τ H} [H, A]^{+} e^{- τ H} B ⟩ d τ \\ = & \int_{0}^{β} ⟨ e^{- τ H} {Be}^{τ H} [H, A]^{+} ⟩ d τ = \int_{0}^{β} ⟨ B^{+} (τ) [H, A] ⟩^{☆} d τ = ⟨ B | LA ⟩^{☆} & (78) \end{matrix}

Index (showing section)

: anti-adjoint, 5.4
: anti-linear, 5.4
: anti-unitary, 5.4
: canonical distribution function, 5.1
: Curie's law, 5.5
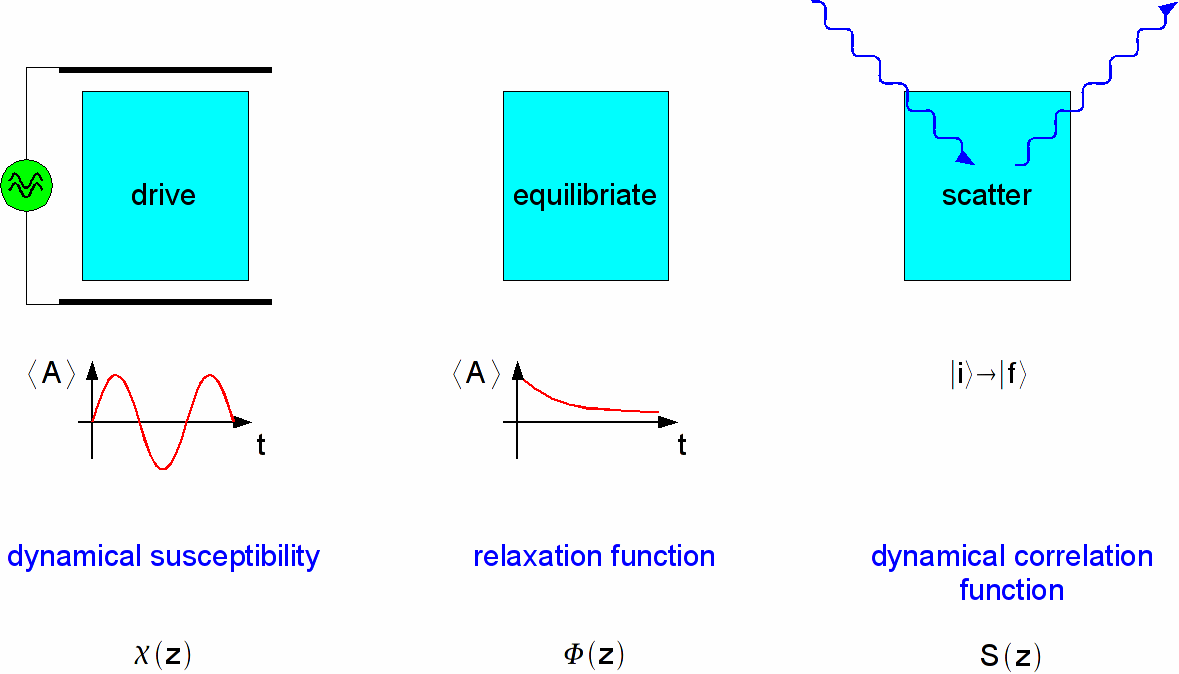
: dynamical susceptibility, 5.2
: imaginary time, 5.5
: inversion, 5.4
: isolated/adiabatic susceptibility, 5.3
: isothermal susceptibility, 5.3
: Kramer-Kronig, 5.3
: microstates, 5.1
: Mori product, 5.5
: non-centro-symmetric, 5.4
: on Neumann's equation, 5.1

: parity, 5.4
: PCT-theorem, 5.4
: retarded/advanced, 5.3
: spectral function, 5.2
: spectral representation, 5.3
: super operator, 5.6
: time inversion, 5.4

File translated from T_EX by T_TM, version 3.85.
On 24 Jan 2010, 21:36.

Contents

List of Figures

5 Linear Response and Dynamical Correlation Functions

5.1 Dynamics of the Statistical Operator: von Neumann's Equation

5.2 Linear Response: Dynamical Susceptibility

5.3 Spectral Representation

5.4 Symmetries

5.5 Mori's Scalar Product

5.6 The Liouville Operator

Index (showing section)